Windsocks
|
|
This picture was taken on Berk kite festival and show some of this "flying objects": two of my windsocks hang up from the kites and two inflated spheres on the ground ( I don't know who made them...) Left side windsock is 8 m long and made by a 150 mm diameter cylinder crossed by some "balls" made with regular polygons. The right one is 16 m long and constructed with a long cone crossed by 8 spiral-made spheres. The spheres on the ground are regular polyhedrons made with regular polygons.
|
On these pages I collected some notes concerning this "flying objects" construction.
There are three basical geometrical solids to make this type of windsocks:
Cylinder.
Sphere.
Cone.
I tried several methods for sphere construction:
With
the multi-faced polyhedrons ( like a ball ).
With
parachute spinnaker cloths..
With
spiral spinnaker cloths..
Cylinder construction
Cylinder is the simplest element because it's possible to make from a fabric rectangle.
Development of cylinder surface is a rectangle with the same height and the width like the cylinder diameter multiplied by pi-greco ( 3.14 )
Cone construction
You can use the cone to join different diameters elements toghether.
You can get the cone development, like as truncated cone, in this mode:
|
|
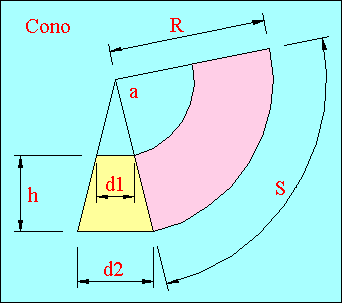
Drawing section of the truncated cone you have to develope, fixing main diameter d2 , smaller diameter d1 and the height h Diameters d2 and d1 have to sets like the different diameters you have toconnect. Height h depend by junction height. Extending both trapeze sides and drawing two circumferences d2 and d1 from intersection point. |
Now it's possible to proceed on two methods:
Marking
out the S
develope
of d2
diameter
, obtaining
this lenght multipling d2
x
3.14.
Measure
circle radius R
and
to obtain the cone develope
angle a
with
this formula:
degree
angle = 180 x d2
/
R
Cone develope is shown in red light color on above picture.
Don't forget to add a 6 mm edge for the sewing.
Sphere construction with parachute spinnaker cloths
This is the construction method for parachutes and bowls.
This geometrical solid is an spherical bowl
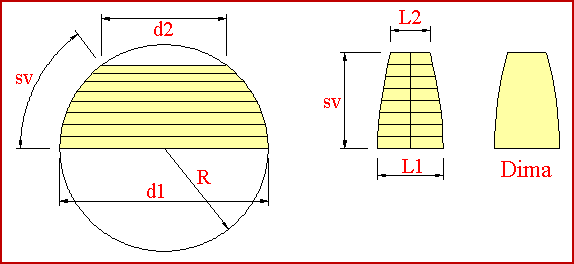
On this picture is shown how to make a spherical sector cardboard
At first you can draw a circle with a radius R like that of the original sphere.
Then you can draw lines d1 and d2 with the same lenght of the two intersecant plane diameters
After this you can measure the circumference development sv and you can divide it by at will number M (8 on shown example)
Then it's possible to draw one vertical line with the same sv-lenght and to divide it by the same number M.
Now you can decide of the number N wich is the number of parts you can choose to divide the spherical bowl.
For each diameter you can calculate the cardboard width with this formula:
L1 = d1 * 3.14 / N ; L2 = d2 * 3.14 / N
and it's the same of the all intermediate diameters.
|
|
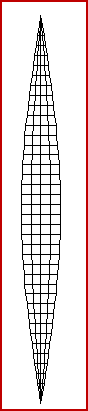
Then you can draw these lenghts on vertical line sv and you can join the line tips with a line wich is the carboard outline. Now you can add a 6 mm hem for the sewings and cut off N-number of identical pieces of fabric. To make a bowl you have to extend one edge of each gore for making an open sock. In this mode you will make spherical bowls with any one dimension and you can to divide in any one number of parts. The left side picture show the spherical development divided by 20 parts. |
Sphere construction with multi-faced polyhedrons
It's
possible to construct a "ball" using regular
polyhedrons.
They are made from many regular polygons like a
football ball.
These polygons are equilateral triangles, squares, pentagons, exagons etc.
With several fabric colors it's possible to obtain interesting effects and you have to make a circular hole on both opposite sides using them in tubolar windsocks .
Here are some interesting polyhedrons and its development.
When you make the construction is verry important to remember the existent connection between the side of polygons and a radius of the sphere inscribed on the polyhedron.
This ratio ( r = edge/radius of the inscribed sphere) help you to decide the polyhedron size.
|
|
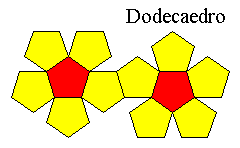
The dodecahedron It's made from 12 pentagons and it's one of most easy to make. Its ratio r is 0.764. This mean that you use 10 cm edge sized pentagons, you will obtain a polyhedron where you can inscribe a sphere with a radius 7.64 cm. |
|---|---|
|
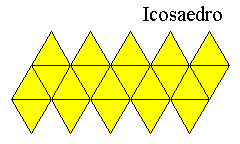
Icosahedron It's made from 20 equilateral triangles and its ratio r is 1.236 |
|
|
|
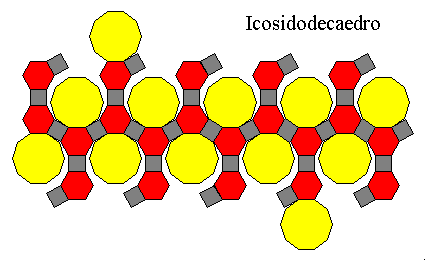
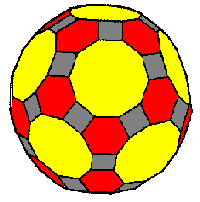
This polyhedron is made by 62 faces: 12 decagons (10 edges polygons), 20 exagons and 30 squares, all with the same edge lenght. The ratio r of this polyhedron is 0.265 On the left picture we can see its development... |
|
..and this is the polyhedron. |
|
|
|
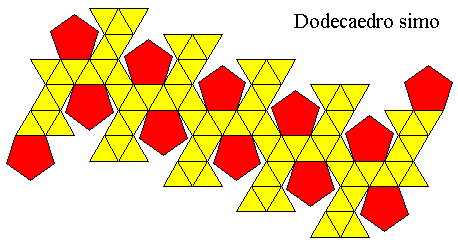
This polyhedron is made by 12 pentagons and 80 equilateral triangles. Its ratio r is 0.477. |
|
And then this is the finosc polyhedron maded by fabric colors wich point out the "star" around all of the pentagons. |
|
|
|
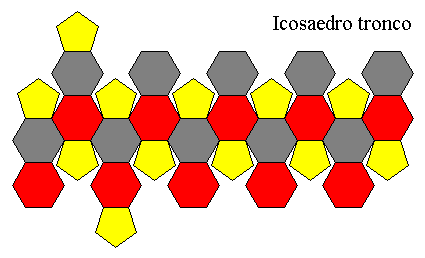
It's made up of 20 exagons and 12 pentagons and its ratio r is 0.412. |
|
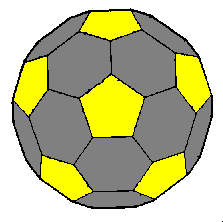
This polyhedron is very known because its leather version had used as football ball... |
|
|
|
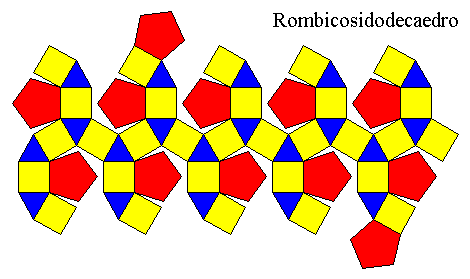
At last, there is a polyhedron made up of 20 equilateral triangles, 30 squares and 12 pentagons. |
|
Its ratio r is 0.46. |
|
|
|
2007 by |
|
e-mail : kites_webmaster@libero.it |
